OpenZFS Capacity Calculator

---

ZFS RAID is not like traditional RAID. Its on-disk structure is far more complex than that of a traditional RAID implementation. This complexity is driven by the wide array of data protection features ZFS offers. Because its on-disk structure is so complex, predicting how much usable capacity you'll get from a set of hard disks given a vdev layout is surprisingly difficult. There are layers of overhead that need to be understood and accounted for to get a reasonably accurate estimate. I've found that the best way to get my head wrapped around ZFS allocation overhead is to step through an example.

We'll start by picking a less-than-ideal RAIDZ vdev layout so we can see the impact of all the various forms of ZFS overhead. Once we understand RAIDZ, understanding mirrored and striped vdevs will be simple. We'll use 14x 18TB drives in two 7-wide RAIDZ2 (7wZ2) vdevs. It will generally be easier for us to work in bytes so we don't have to worry about conversion between TB and TiB.

Starting with the capacity of the individual drives, we'll subtract the size of the swap partition. The swap partition acts as an extension of the system's physical memory pool. If a running process needs more memory than is currently available, the system can unload some of its in-memory data onto the swap space. By default, TrueNAS CORE creates a 2GiB swap partition on every disk in the data pool. Other distributions may create a large or smaller swap partition or might not create one at all.

18 * 1000^4 - 2 * 1024^3 = 17997852516352 bytes

Next, we want to account for reserved sectors at the start of the disk. The layout and size of these reserved sectors will depend on your operating system and partition scheme, but we'll use FreeBSD and GPT for this example because that is what's used by TrueNAS CORE and Enterprise. We can check sector alignment by running gpart list on one of the disks in the pool:

We'll first note that the sector size used on this drive is 512 bytes. Also note that the first logical block on this disk is actually sector 40; that means we're losing 40 * 512 = 20480 bytes right there.

The Name: da1p1 section describes the swap partition on this drive. We can see it's 2GiB in size (as expected) and it starts at logical block address 128 (i.e., an offset of 512 * 128 = 65536 bytes). If we subtract this lost space from the expected partition size calculated above, we see it lines up with the actual on-disk partition size:

17997852516352 - 20480 - 65536 = 17997852430336 bytes

Before ZFS does anything with this partition, it rounds its size down to align with a 256KiB block. This rounded-down size is referred to as the osize or physical volume size of the disk in the ZFS code.

floor(17997852430336 / (256 * 1024)) * 256 * 1024 = 17997852311552 bytes

Inside the physical ZFS volume, we need to account for the special labels added to each disk. ZFS creates 4 copies of a 256KiB vdev label on each disk (2 at the start of the ZFS partition and 2 at the end) plus a 3.5MiB embedded boot loader region. Details on the function of the vdev labels can be found here and details on how the labels are sized and arranged can be found here and in the sections just below this (lines 541 and 548). We subtract this 4.5MiB (4x 256KiB + 3.5MiB) of space from the ZFS partition to get its "usable" size:

17997852311552 - 4 * 262144 - 3670016 = 17997847592960 bytes

Next up, we need to calculate the allocation size or "asize" of the whole vdev. We simply multiply the usable ZFS partition size by the vdev width here. We're not accounting for parity space just yet:

17997847592960 * 7 = 125984933150720 bytes

That's about 114.58 TiB. ZFS takes this chunk of storage represented by the allocation size and breaks it until smaller, uniformly-sized buckets called "metaslabs". ZFS creates these metaslabs because they're much more manageable than the full vdev size when tracking used and available space via spacemaps. The size of the metaslabs are primarily controlled by the metaslab shift or "ms_shift" variable with the target size being 2^ms_shift bytes. You can read more about metaslab sizing here.

ZFS sets ms_shift so that the quantity of metaslabs is under 200. ms_shift starts at 29 and grows as high as 34. Once ms_shift is 34, it doesn't grow any larger but instead the metaslab count grows beyond 200. 2^17 or 131,072 is the cap on the metaslab count (or ms_count); after that cap is hit, ZFS allows metaslabs to grow larger than 16 GiB. You won't hit this cap until your vdev allocation size is at least 2^17 * 16 GiB = 2 PiB. Again, that's the size of an individual vdev, not the whole pool; you aren't going to run into this unless you put more than 125 18TB disks in a single vdev (which is actually possible with dRAID). If you do exceed 131,072 metaslabs, ZFS will increase the ms_shift value until you're back under it again. OpenZFS can handle metaslab shift values up to 64.

On the other hand, the "cutoff" for going from ms_shift = 34 down to ms_shift = 33 is really pretty small, 1,600GiB or 1.5625TiB. In other words, unless your vdevs are smaller than 1.5625TiB, your pool's ms_shift value will be 34. For our example, asize is well over 1.5625TiB so we have ms_shift = 34.

Once we have the value of ms_shift we can easily calculate the metaslab size by doing 2^ms_shift.

2 ^ 34 = 17179869184 bytes

With ms_shift = 34, the metaslab size will be 16GiB. We can note that if ms_shift was 33, the metaslab size would be 8GiB; the metaslab size gets cut in half each time ms_shift decreases by 1. We now need to figure out how many full 16GiB metaslabs will fit in each vdev, so we calculate asize / metaslab_size and round down using the floor() function (the 16GiB metaslab size is represented in bytes below):

floor(125984933150720 / 17179869184) = 7333

This gives us 7,333 metaslabs per vdevs. We can check our progress so far on an actual ZFS system by using the zdb command provided by ZFS. We can check vdev asize and the metaslab shift value by running zdb -C $pool_name and we can check metaslab count by running zdb -m $pool_name. Note on TrueNAS, you'll need to add the -U /data/zfs/zpool.cache option (i.e., zdb -U /data/zfs/zpool.cache -C $pool_name and zdb -U /data/zfs/zpool.cache -m $pool_name).

To calculate useful space in our vdev, we multiply the metaslab size by the metaslab count. This means that space within the ZFS partition but not covered by one of the metaslabs isn't useful to us and is effectively lost. In theory, by using a smaller ms_shift value, we could recover a bit of this space, but we would end up using a lot more system memory so it's not really worth it. With 7,333 metaslabs at 16GiB per metaslab, we have:

17179869184 * 7333 = 125979980726272 bytes

That's about 114.58 TiB of useful space per vdev. If we multiply that by the quantity of vdevs, we get the ZFS pool size:

125979980726272 * 2 = 251959961452544 bytes

We can confirm this by running zpool list:

The -p flag shows exact (parsable) byte values and the -o flag determines what properties will be displayed.

Note that the zpool SIZE value matches what we calculated above. We're going to set this number aside for now and calculate RAIDZ parity and padding. Before we proceed, it will be helpful to review a few ZFS basics including ashift, minimum block size, how partial-stripe writes work, and the ZFS recordsize value.

Hard disks and SSDs divide their space into tiny logical storage buckets called "sectors". A sector is usually 4KiB but could be 512 bytes on older hard drives or 8KiB on some SSDs. A sector represents the smallest read or write a disk can do in a single operation. ZFS tracks disks' sector size as the "ashift" where 2^ashift = sector size (so ashift = 9 for 512 byte sectors, 12 for 4KiB sectors, 13 for 8KiB sectors).

In RAIDZ, the smallest useful write we can make is p+1 sectors wide where p is the parity level (1 for RAIDZ1, 2 for Z2, 3 for Z3). This gives us a single sector of user data and however many parity sectors we need to protect that user data. With this in mind, ZFS allocates space on RAIDZ vdevs in even multiples of this p+1 value. It does this so we don't end up with unusable-small gaps on the disk. For example, imagine we made a 5-sector write to a RAIDZ2 vdev (3 user data sectors and 2 parity sectors). We later delete that data and are left with a 5-sector gap on the disk. We now make a 3-sector write to the Z2 vdev, it lands in that 5-sector gap and we're left with a 2-sector gap that we can't do anything with. That space can't be recovered without totally rewriting every other sector on the disk after it.

To avoid this, ZFS will pad out all writes to RAIDZ vdevs so they're an even multiple of this p+1 value. By "pad out" we mean it just logically includes these extra few sectors in the block to be written but doesn't actually write anything to them. The ZFS source code refers to them as "skip" sectors.

Unlike traditional RAID5 and RAID6 implementations, ZFS supports partial-stripe writes. This has a number of important advantages but also presents some implications for space calculation that we'll need to consider. Supporting partial stripe writes means that in our 7wZ2 vdev example, we can support a write of 12 total sectors even though 12 is not an even multiple of our stripe width (7). 12 is evenly divisible by p+1 (3 in this case), so we don't even need any padding. We would have a single full stripe of 7 sectors (2 parity sectors plus 5 data sectors) followed by a partial stripe with 2 parity sectors and 3 data sectors. This will be important because even though we can support partial stripe writes, every stripe (including those partial stripes) need a full set of p parity sectors.

The last ZFS concept we need to understand here is the recordsize value. The ZFS recordsize value is used to determine the largest block of data ZFS can write out. It can be set per-dataset and can be any even power of 2 from 512 bytes up to 16MiB (values above 1MiB require changing the zfs_max_recordsize kernel module parameter). The default recordsize value is 128KiB. For capacity estimation purposes, ZFS always assumes a 128KiB record. It's important to note that this recordsize value only considers user data, not parity or padding. It's also worth mentioning that block sizes in ZFS will vary based on how much data needs to be written out and the recordsize value enforces the upper limit of that block size, but again, ZFS assumes all 128KiB records for space calculation purposes, so we're going to use that value going forward.

You can read more about ZFS' handling of partial stripe writes and block padding in this article by Matt Ahrens.

Getting back to our capacity example, we have the minimum sector count already calculated above at p+1 = 3. Next, we need to figure out how many sectors will get filled up by a recordsize write (128KiB here).

128 * 1024 / 4096 = 32 sectors

Our stripe width is 7 disks, so we can figure out how many stripes this 128KiB write will take. Remember, we need 2 parity sectors per stripe, so we divide the 32 sectors by 5 because that's the number of data sectors per stripe:

32 / (7-2) = 6.4

We can visualize how this might look on the disks (P represents a parity sectors, D represents a data sectors):

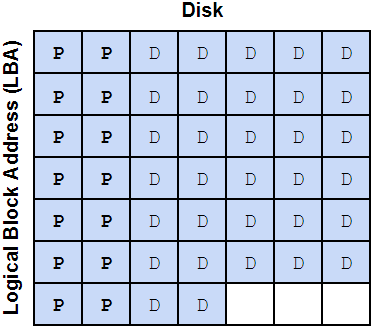
As mentioned above, that partial 0.4 stripe also gets 2 parity sectors, so we have 7 stripes of parity data at 2 parity sectors per stripe, or 14 total parity sectors. We now have 32 data sectors, 14 parity sectors, adding those, we get 46 total sectors for this data block. 46 is not an even multiple of our minimum sector count (3), so we need to add 2 padding sectors. This brings our total sector count to 48: 32 data sectors, 14 parity sectors, and 2 padding sectors.

With the padding sectors included, this is what the full 128KiB block might look like on disk. I've drawn two blocks so you can see how alignment of the second block gets shifted a bit to accommodate the partial stripe we've written. The X's represent the padding sectors.

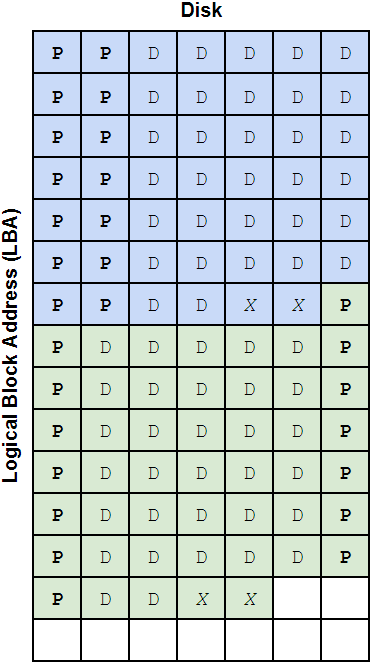
This probably looks kind of weird because we have one parity sector at the start of the second block just hanging out by itself, but even though it's not on the same exact row as the data it's protecting, it's still providing that protection. ZFS knows where that parity data is written so it doesn't really matter what LBA it gets written to, as long as it's on the correct disk.

We can calculate a data storage efficiency ratio by dividing our 32 data sectors by the 48 total sectors it takes to store them on disk with this particular vdev layout.

32 / 48 = 0.66667

ZFS uses something similar to this ratio when allocating space but in order to simplify calculations and avoid multiplication overflows and other weird stuff it tracks this ratio as a fraction of 512. In other words, to more accurately represent how ZFS "sees" the on-disk space, we need to convert the 32/48 fraction to the nearest fraction of 512. We'll need to round down to get a whole number in the numerator (the top part of the fraction). To do this, we calculate:

floor(0.66667 * 512) / 512 = 0.666015625 = 341/512

This 341/512 fraction is called the vdev_deflate_ratio and it's what we'll multiply the pool size calculated above by to get usable space per vdev after parity and padding. You can read a bit more on the vdev_deflat_ratio here.

251959961452544 * 0.666015625 = 167809271201792 bytes

The last thing we need to account for is SPA slop space. ZFS reserves the last little bit of pool capacity "to ensure the pool doesn't run completely out of space due to unaccounted changes (e.g. to the MOS)". Normally this is 1/32 of the usable pool capacity with a minimum value of 128MiB. OpenZFS 2.0.7 also introduced a maximum limit to slop space of 128GiB (this is good; slop space used to be HUGE on large pools). You can read about SPA slop space reservation here.

For our example pool, slop space would be...

167809271201792 * 1/32 = 5244039725056 bytes

That's 4.77 TiB reserved... again, a TON of space. If we're running OpenZFS 2.0.7 or later, we'll use 128 GiB instead:

167809271201792 - 128 * 1024^3 = 167671832248320 bytes = 156156.5625 GiB = 152.4966 TiB

And there we have it! This is the total usable capacity of a pool of 14x 18TB disks configured in 2x 7wZ2. We can confirm the calculations using zfs list:

As with the zpool list command, the -p flag shows exact byte values.

167671831168032 + 1080288 = 167671832248320 bytes = 156156.5625 GiB = 152.4966 TiB

By adding the USED and AVAIL values, we can confirm that our calculation is accurate.

Mirrored vdevs work in a similar way but the vdev asize is just a single drive's capacity (minus ZFS labels and whatnot) and then the vdev_deflate_ratio is just 512/512 or 1.0. We skip all the parity and padding sector stuff but we do still need to account for metaslab allocation and SPA slop space.

dRAID Capacity Calculation

Capacity calculation for dRAID vdevs is similar to that of RAIDZ but includes a few extra steps. We'll run through an abbreviated example calculation with 2x dRAID2:5d:20c:1s with 8TB disks (no swap space reserved this time).

dRAID still aligns the space on each drive to a 256KiB block size, so we go from 8000000000000 bytes to 7999999967232 bytes per 8TB disk:

floor(8000000000000 / (256 * 1024)) * 256 * 1024 = 7999999967232 bytes

From there, we reserve space for the on-disk ZFS labels (just like in RAIDZ) but we also reserve an extra 32MiB for dRAID reflow space which is used when expanding a dRAID vdev. Details on the reflow reserve space can be found here.

7999999967232 - (256 * 1024 * 4) - (7 * 2^19) - 2^25 = 7999961694208 bytes

dRAID does not support partial stripe writes so we go through several extra alignment operations to make sure our capacity is an even multiple of the group width. Group width in dRAID is defined as the number of data disks in the configuration plus the number of parity disks. For our configuration, that's 5 + 2 = 7 disks. dRAID allocates 16MiB of space from each disk in the group to form a row (details here), so we can multiply the row height (16 MiB) by the group width (7) to get the group size:

7 * 16 * 1024^2 = 117440512 bytes

First we align the individual disk's allocatable size to the row height (16 MiB):

floor(7999961694208 / (16 * 1024^2)) * 16 * 1024^2 = 7999947014144 bytes

To get the total allocatable capacity, we multiply this by the number of child disks minus the number of spare disks in the vdev:

7999947014144 * (20 - 1) = 151998993268736 bytes

And then this number is aligned to the group size which we calculated above:

floor(151998993268736 / 117440512) * 117440512 = 151998909382656 bytes

This is the allocatable size (or asize) of each of our two dRAID vdevs. We go through the same logic as RAIDZ used to determine the metaslab count but each metaslab gets its size adjusted so its starting offset and its overall size lines up with the minimum allocation size. The minimum allocation size is the group width times the sector size (or 2^ashift). For our layout that is:

7 * 2^12 = 28672 bytes

This represents the smallest write operation we can make do our layout. To align the metaslabs, ZFS iterates over each one, rounds the starting offset up to align with the minimum allocation size, then rounds the total size of the metaslab down so its evenly divisible by the minimum allocation size. Detail on dRAID's metaslab initialization process can be found here and the code for the process is simplified and mocked up below:

Each metaslab will get a bit of space trimmed off its head and/or its tail. The table below shows the results from the first 20 iterations of the above loop:

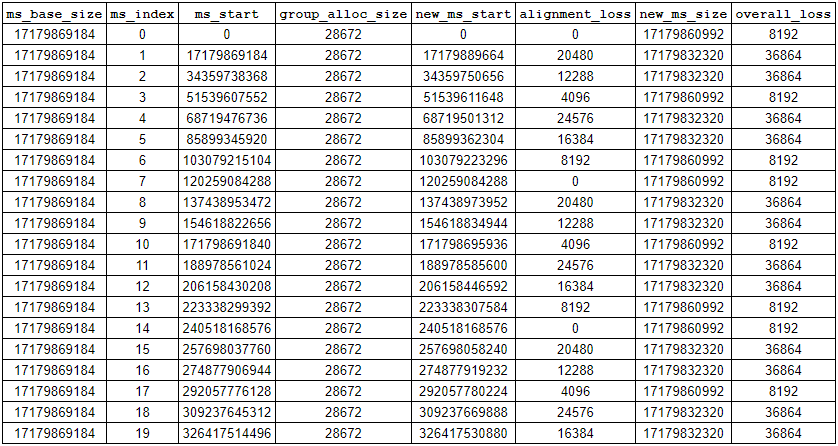
As you can see, we'll end up with some lost space in between many of the metaslabs but it's not very much (at worst, a few gigabytes for multi-PB sized pool). You'll also notice that the metaslab size isn't uniform across the pool; that makes it very hard (maybe impossible) to write a simple, closed-form equation for vdev_raw_size without a loop or summation. Note that for some dRAID topologies, the metaslabs just happen to line up without any shifting and every metaslab is exactly 2^ms_shift and we don't lose any extra space, but that's not very common.

If you're inclined, you can validate this non-uniform metaslab sizing using zdb -m tank. If you pull the offset listed with each metaslab and convert it from hex to decimal, you can calculate its size. You'll see the size for each metaslab varies slightly as the above table shows. zdb -m also lists the metaslab size, but it rounds it to the nearest tenth of a GiB which is not a fine enough resolution to see the tiny sizing variations.

As a side note, we could theoretically shift the first metaslab's offset to align with the minimum allocation size and then size it down so its overall size was an even multiple of the minimum allocation size and all subsequent metaslabs (each sized down uniformly to be an even multiple of the min alloc size) would naturally line up where they needed to with no gaps in between. In order to do this, however, the OpenZFS developers would need to add dRAID specific logic to higher-level functions in the code; they opted to keep it simple. The amount of usable space lost to those gaps between the shifted metaslabs really is negligible though, like on the order of 0.00004% of overall pool space.

Once we have the vdev_raw_size, we need to calculate the deflate ratio for our dRAID vdevs. This follows a very similar process to RAIDZ deflate ratio calculation but it's a bit simpler because we don't need to account for partial stripe parity sectors (because we don't have any partial stripes!)

We start with the recordsize (which we'll assume is the default 128KiB) and figure out how many sectors (each sized at 2^ashift) it takes to store a block of this size:

128 * 1024 / 2^12 = 32 sectors

Then we figure out how many redundancy groups this will fill by dividing it by the number of data disks per redundancy group (not the total group width, just the data disks; parity disks don't store data!):

32 / 5 = 6.4

We can't fill a partial redundancy group so we round up to 7. We then multiply this by the redundancy group width (including parity) to get the total number of sectors it takes to store the 128KiB block:

7 * 7 = 49

This configuration consumes 49 total sectors to store 32 sectors worth of data, giving us a ratio of

32 / 49 = 0.6531...

Just like with RAIDZ, we round this down to be a whole fraction of 512 to get the deflate ratio:

floor( (32 / 49) * 512 ) / 512 = 0.6523...

We end up with 334/512 (or 0.6523...) as the deflate ratio for this configuration. We multiply the vdev_raw_size by the vdev count and the deflate ratio to get our pool usable size before slop:

151990085230592 * 2 * 334/512 = 198299564324288 bytes

We compute slop space the same as we did above (we exceed the max here so we use 128 GiB) and remove that from our usable space to get final, total usable for this pool:

198299564324288 - (128 * 1024^3) = 198162125370816 bytes

We can validate this with zfs list:

By adding the values in USED and AVAIL, we can confirm our calculations are accurate:

4545072 + 198162120825744 = 198162125370816 bytes = 184552.86 GiB = 180.23 TiB

Closing Thoughts

The RAIDZ example used VirtualBox with virtual 18TB disks that hold exactly 18,000,000,000,000 bytes. Real disks won't have such an exact physical capacity; the 8TB disks in my TrueNAS system hold 8,001,563,222,016 bytes. If you run through these calculations on a real system with physical disks, I recommend checking the exact disk and partition capacity using gpart or something similar.

We took a shortcut with the dRAID example because we didn't need to include swap space. We used truncate to create sparse files to mimic 8TB disks. The syntax for the dRAID example is below:

You can optionally mount these files as loop devices with losetup. You can set the apparent sector size of the loop device as well so you don't need to specify the ashift value when creating your pool.

It's worth noting that none of these calculations factor in any data compression. The effect of compression on storage capacity is almost impossible to predict without running your data through the compression algorithm you intend to use. At iX, we typically see between 1.2:1 and 1.6:1 reduction assuming the data is compressible in the first place. Compression in ZFS is done per-block and will either shrink the block size a bit (if the block is smaller than the recordsize) or increase the amount of data in the block (if the block is equal to the recordsize).

We're also ignoring the effect that variable block sizes will have on functional pool capacity. We used a 128 KiB block because that's the ZFS default and what it uses for available capacity calculations, but (as discussed above) ZFS may use a different block size for different data. A different block size will change the ratio of data sectors to parity+padding sectors so overall storage efficiency might change. The calculator above includes the ability to set a recordsize value and calculate capacity based on a pool full of blocks that size. You can experiment with different recordsize values to see its effects on efficiency. Changing a dataset's recordsize value will have effects on performance as well, so read up on it before tinkering. You can find a good high-level discussion of recordsize tuning here, a more detailed technical discussion here, and a great generalized workload tuning guide here on the OpenZFS docs page.

Please feel free to get in touch with questions or if you spot any errors! jason@jro.io

If you're interested in how the pool annual failure rate values are derived, I have a write-up on that here.

(Click table cells above to freeze/unfreeze)